PROPIEDADES DE LOS RADICALES
Propiedades de las Raices
Debido a que las raíces pueden convertirse a potencias de exponente fraccionario, cumplen con todas las propiedades de potencias a partir de las cuales se pueden deducir las siguientes propiedades de raíces:
1) Multiplicación de raíces de igual índice:
Se multiplican las bases y se conserva el índice.
2) División de raíces de igual índice:
Se dividen las bases y se conserva el índice.
3) Raíz de raíz:
Para obtener raíz de raíz se multiplican los índices y se conserva la base.
4) Raíz de una potencia cuyo exponente es igual al índice:
Exponente e índice se anulan entre sí, por lo tanto desaparece el radical y la base queda aislada.
5) Propiedad de amplificación:
Tanto el índice como el exponente de la potencia pueden amplificarse por un mismo valor.
6) Ingreso de un factor dentro de una raíz:
(con la restricción que a>0 si n es par)
Para introducir un factor dentro de una raíz se coloca el factor dentro del radical como potencia con exponente igual al índice y multiplicando a los demás factores.
Observación: las propiedades anteriores son válidas solamente en el caso de que las raíces estén definidas en los números reales.
Calcula los valores de las siguientes potencias:
1
2
3
4
Efectuar:
1![Rendered by QuickLaTeX.com \sqrt{\sqrt[3]{\sqrt[4]{2}}}](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-df833cc16ec4fefc98ed394d7dcd9ad0_l3.png)
2![Rendered by QuickLaTeX.com \sqrt{2\sqrt[3]{2 \sqrt[4]{2}}}](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-27670bcbd747c7d497c7a4c69ebb490f_l3.png)
3![Rendered by QuickLaTeX.com \sqrt{\sqrt[3]{\sqrt{\sqrt[3]{2 \sqrt{2}}}}}](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-209f1631420eee992764cfe33054c285_l3.png)
Simplificar las expresiones al máximo, racionalizando el resultado si es necesario.
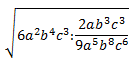
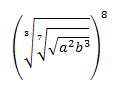

Comentarios
Publicar un comentario