CÁLCULO DE PORCENTAJES

Observa la explicación que ofrece el vídeo acerca de cómo calcular porcentajes.

El porcentaje representa una parte de un total.

Por ejemplo: una tarta se divide en 2 partes y tomamos 1, el porcentaje que esto representa sería:

1 / 2 = 0,5

 El porcentaje se representa en tantos por 100, que se calcula multiplicando el resultado obtenido por 100.

0,5 x 100 = 50%

 Para calcular un porcentaje (A) de un número (B) se aplica la fórmula:

A% de B = (A x B) / 100

Ejemplo: calcula el 20% de 60:

20% de 60 = (20 x 60) / 100 = 12

 

a) Aumentos porcentuales

Para incrementar una cantidad en un porcentaje, primero calculamos lo que representa el porcentaje de esa cantidad y luego se lo sumamos a dicha cantidad.

Ejemplo: incrementa 150 en un 20%.

Calculamos cuanto es un 20% de 150:

20% de 150 = (20 x 150) / 100 = 30

Este importe se lo sumamos al importe inicial:

150 + 30 = 180

 

Otro problema que se puede plantear es una cantidad varía de un importe inicial a un importe final y queremos saber en qué porcentaje se ha incrementado.

Por ejemplo, un automóvil que valía 12.000 euros ha incrementado su precio a 13.500 euros. ¿Qué porcentaje se ha incrementado?

 Se calcula aplicando la fórmula:

% variación = (Importe final - Importe inicial) x 100 / Importe inicial

En el ejemplo:

% variación = (13.500 – 12.000) x 100 / 12.000 = 12,5%

 b) Disminuciones porcentuales

Para disminuir una cantidad en un porcentaje, calculamos lo que representa el porcentaje de dicha cantidad y luego se lo restamos.

Ejemplo: disminuye 90 en un 40%.

Calculamos cuanto es un 40% de 90:

40% de 90 = (40 x 90) / 100 = 36

Este importe se lo restamos al importe inicial:

90 - 36 = 54

 

Al igual que en el caso anterior, se puede plantear el problema de una cantidad que disminuye de un importe inicial a un importe final y queremos saber en qué porcentaje lo ha hecho.

Por ejemplo, un televisor que valía 900 euros ahora cuesta 720 euros. ¿Qué porcentaje ha disminuido?

Se aplica la misma fórmula que en el punto anterior:

% variación = (Importe final - Importe inicial) x 100 / Importe inicial

En el ejemplo:

% variación = (720 – 900) x 100 / 900 = -20%

 

c) Repartos proporcionales

Tres amigos salen a pasear: el primero toma 3 helados, el segundo 2 helados y el tercero 1 helado. El total de la consumición es 36 euros ¿Cuánto tiene que pagar cada uno?

No podemos dividir el importe entre 3 porque cada uno de ellos ha tomado un número diferente de helados.

Para realizar un reparto proporcional, en función del número de helados tomados, aplicamos una regla de 3 simple:

Entre los 3 amigos han tomado 6 helados:

El primero de los amigos ha tomado 3:

6 helados ------> 36 euros
3 helados ------>“a” euros

Siendo “a” = (36 x 3) / 6 = 18 euros tiene que pagar el primer amigo

El segundo de los amigos ha tomado 2:

6 helados ------> 36 euros
2 helados ------>“b” euros

Siendo “b” = (36 x 3) / 6 = 12 euros euros tiene que pagar el segundo amigo

El tercero de los amigos tan sólo ha tomado 1:

6 helados ------> 36 euros
1 helados ------>“c” euros

Siendo “c” = (36 x 1) / 6 = 6 euros euros tiene que pagar el tercer amigo.

Problemas con Porcentajes 

En una clase hay un total de 25 alumnos. Han aprobado matemáticas el 64%. ¿Cuántos alumnos han suspendido?

Respuesta: 9 alumnos

Solución:

Hallamos el número de alumnos que han aprobado: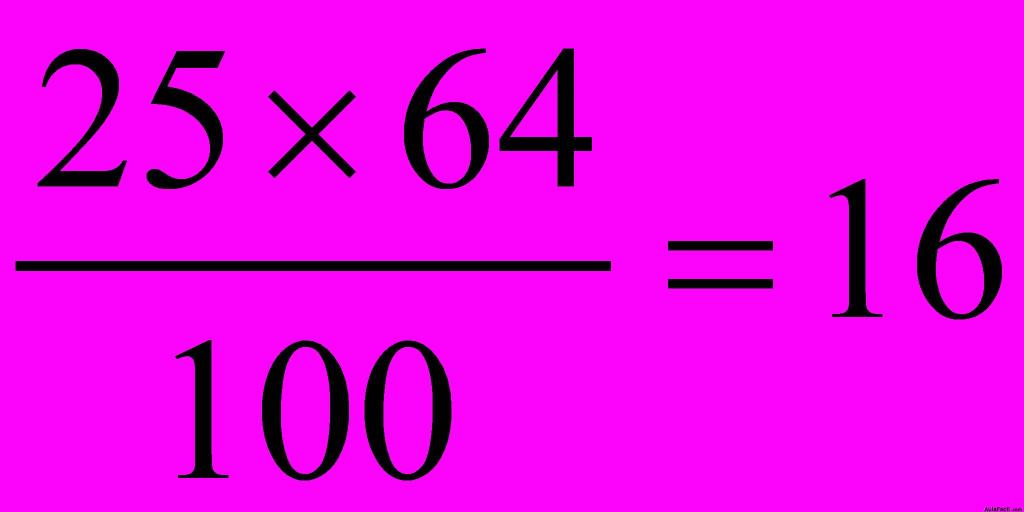

Habrán suspendido: 25 – 16 = 9 alumnos.

Un par de zapatos costaron hasta ayer 36 €. A partir de hoy van a descontar un 10%. ¿Cuánto pagaré por ellos?

Respuesta: 32,40 €

Solución:

Debo calcular el 10% de 36: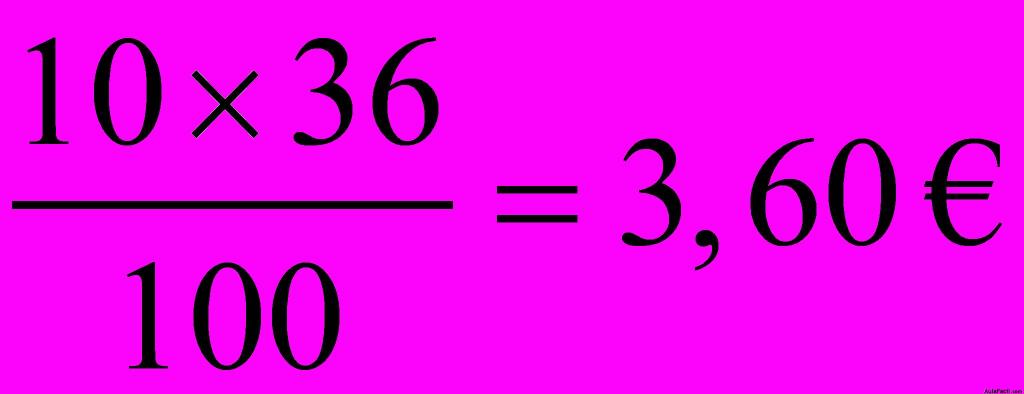   
Si me descuentan 3,60 € debo pagar: 36 – 3,60 = 32,40 €

He comprado un libro que lleva el precio de 15 € y a la hora de pagar, el librero me cobra 16,05 €. ¿Se ha equivocado?

 En un bosque el 65% de los árboles que hay son pinos. El número de árboles es de 12000. ¿Cuántos pinos hay?

Respuesta: 7800 pinos.

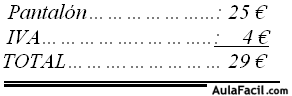
Un pantalón sin IVA vale 25 €. Si el impuesto del IVA es del 16% ¿Cuánto tengo que pagar por él?

Respuesta: 29 €

Solución:

Calculo a cuanto asciende el IVA: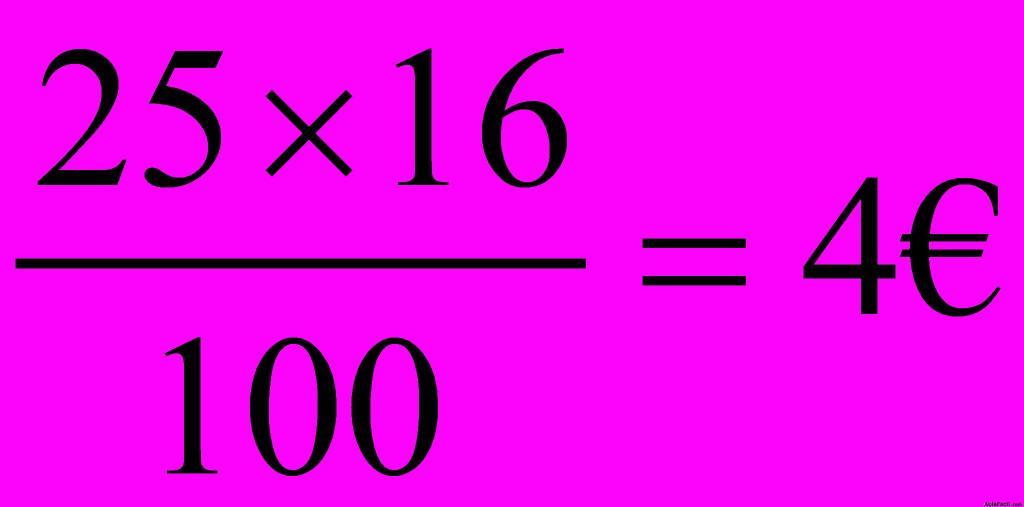  
Debo pagar:

             

CALCULAR:

• 1. El 15% de 40 es:

A) 60
B) 34
C) 6
D) 0.6

• 2. Hallar el 30% de 280

A) 21
B) 4.2
C) 196
D) 84

• 3. De un salòn de 60 alumnos el 25% reprueba matemática, ¿Cuántos alumnos aprueban matemática?

A) 35
B) 45
C) 55
D) 40

• 4. Si mi 100% es 13.8. Hallar el 35%

A) 8.97
B) 14
C) 4.83
D) 39.42

• 5. En una canasta hay 80 manzanas, de las cuales se malogran el 40%. ¿Cuántas manzanas están en buen estado?

A) 32
B) 58
C) 64
D) 48

• 6. Si el 20% de una cantidad es 8, calcular dicha cantidad

A) 1.6
B) 40
C) 6.4
D) 8

• 7. Halla el 5% 32 000

A) 30400
B) 16000
C) 160
D) 1600

• 8. Una camisa cuesta 160 pesos, si la vendedora me descuenta el 20%, ¿Cuánto es lo que le debo pagar?

A) $32
B) $12.8
C) $128
D) $3.2

• 9. Encuentra cuánto me costará una pantalla plana que tiene el 25% de descuento y su costo inicial es de $12,580

A) $314.50
B) $3,145
C) $9,435
D) $10,693

• 10. Si el 30% de un número es 12, ¿Cuál es el 25% de dicho número?

A) 10
B) 40
C) 20
D) 60

• 11. El primer día de clases, había 835 alumnos en una secundaria; al finalizar la semana eran ya 1002. ¿En qué porcentaje aumentó la población de esa escuela?

A) 140
B) 20%
C) 120%
D) 83.33%

• 12. Berenice ayudó a su papá a vender pollo a domicilio durante sus vacaciones. Él ofreció a la niña el 15% de todo lo que ella vendiera. Si al finalizar el verano Berenice había vendido $735.5, ¿Cuánto le pagó su papá?

A) $735.50
B) $625.175
C) $110.325
D) $4,903.333

• 13. El número de alumnos de una escuela descendió de 510 a 440. Expresa en porcentaje esta reducción.

A) 15.90%
B) 115.90%
C) 86.27%
D) 13.73%

• 14. María compró, en una venta de saldos, mercancía por $4,375. Si al vender esa mercancía obtuvo una cantidad de $5,425 ¿Qué porcentaje obtuvo de ganancia?

A) 24%
B) 19.35%
C) 124%
D) 80.65%