FUNCIONES RACIONALES

 














 Como cualquier fracción, una expresión racional puede simplificarse. Para simplificar una expresión racional, necesitarás factorizar los polinomios, determinar si algún factor es igual a otro y luego, cancelar todos los factores similares.

Fracción: 915=3⋅33⋅5=35

Expresión Racional: x2+6x+9x2+8x+15=(x+3)(x+3)(x+3)(x+5)=x+3x+5

En ambas fracciones separamos el numerador y el denominador en una factorización de primos. Luego, cancelamos los factores comunes.

Nota Importante: x+3x+5 está factorizado completamente. No canceles las x . 3x5x se 

reduce a 35 , pero x+3x+5 no lo hace debido al signo de suma. Para probar esto, 

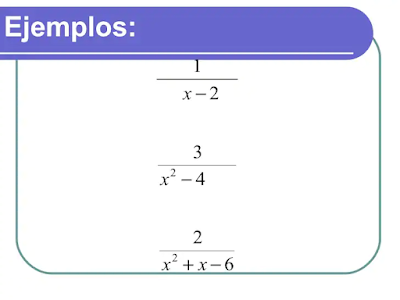
reemplazaremos un número por x para demostrar que la fracción no se reduce a 35 . Si x=2 , entonces 2+32+5=57≠35 .

Ejemplo A

Simplifica 2x34x2−6x .

Solución: Los factores del numerador son 2x3=2⋅x⋅x⋅x y el denominador es 4x2−6x=2x(2x−3) .

2x34x2−6x=2⋅x⋅x⋅x2⋅x⋅(2x−3)=x22x−3

Ejemplo B

Simplifica 6x2−7x−32x3−3x2 .

Solución: Si necesitas revisar la factorización, ve a la sección Factorización de Cuadráticos Cuando el Coeficiente Principal es 1 y a la sección Factorización de Cuadráticos Cuando el Coeficiente Principal no es 1. Si no, factoriza el numerador y encuentra el MCD del denominador y cancela los términos similares.

6x2−7x−32x3−3x2=(2x−3)(3x+1)x2(2x−3)=3x+1x2

Ejemplo C

Simplifica x2−6x+272x2−19x+9 .

Solución: Factoriza la parte superior y la inferior y ve si hay algún factor común.

x2−6x+272x2−19x+9=(x−9)(x+3)(x−9)(2x−1)=x+32x−1

A TRABAJAR CON LO APRENDIDO:

1.-Representar las hipérbolas de ecuación  y= 8  e  y =-8 
                     .                                                       x             x   

2.-Representa la hipérbola de ecuación  y= 12 . Indica las asíntotas y 
                                x
el centro de la misma.


3.-



4.-Determinar las asíntotas de las siguientes funciones


5.- Simplificar las siguientes funciones racionales

1. 3x2−x3x2

2. x2+6x+8x2+6x+9

3. 2x2+x−106x2+17x+5

  1. 4x32x2+3x
  2. x3+x2−2xx4+4x3−5x2
  3. 2x2−5x−32x2−7x−4
  4. 5x2+37x+145x3−33x2−14x
  5. 8x2−60x−32−4x2+26x+48
  6. 6x3−24x2+30x−1209x4+36x2−45
  7. 6x2+5x−46x2−x−1
  8. x4+8xx4−2x3+4x2
  9. 6x4−3x3−63x212x2−84x
  10. x5−3x3−4xx4+2x3+x2+2x
  11. −3x2+25x−8x3−8x2+x−8

  12. 3    +3x2+13x−15    −2x3+7x2+20x−25





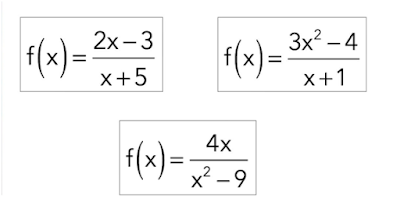
Comentarios

Publicar un comentario

Entradas más populares de este blog

Propiedades de la potenciación de números enteros

Imagen
Entonces, multiplicar potencias de igual base equivale a poner la misma base y sumar los exponentes. RESUELVE AHORA: ENTONCES, DIVIDIR POTENCIAS DE IGUAL BASE EQUIVALE A PONER LA MISMA BASE Y RESTAR LOS EXPONENTES.- Escribe en tu cuaderno los siguientes cocientes en forma de potencia:     a) 2 7  : 2 3           b) 3 5  : 3 3           c) 5 6  : 5 3 TIENES QUE SABER QUE SE PUEDE EXPRESAR LA DIVISIÓN DE POTENCIAS DE OTRA MANERA Y LA FORMA DE RESOLVER CUANDO TIENEN LA MISMA BASE, ES LA MISMA. AHORA OBSERVA  ASÍ, SI TENEMOS UNA POTENCIA ELEVADA A EXPONENTE, ES IGUAL A PONER LA MISMA BASE Y MULTIPLICAR LOS EXPONENTES. Escribe en tu cuaderno las siguientes potencias en forma de potencia con un solo exponente:     a) (2 3 ) 7           b) (3 5 ) 3           c) (5 5 ) 3 También podes acceder a: https://es.slideshare.net/logosacademyeduec/potenciacion-propiedades-eduardo Efectúa adecuadamente en tu cuaderno cada cas
Leer más

Ejercicios combinados con números decimales periódicos

Imagen
                                                                                                                             Realizar las siguientes operaciones realizando primero pasaje de decimal a fracción:   1)     2)     3)   Podés mandar tus resultados a luciasigrist@hotmail.com o ponerlos en comentarios y te los respondo.                                        
Leer más

Operaciones combinadas con potencias y raíces de fracciones

Imagen
Miramos detenidamente los vídeos, nos detenemos y hasta retrocedemos, en caso de no entender algo y después de haber comprendido o eliminado la duda, recién avanzar. No olvides escribir el o los ejercicios que se proponen en los vídeos en tu cuaderno, e ir resolviendo junto con el profesor.                                             Ahora resuelve:                                         Podés mandar tus resultados a luciasigrist@hotmail.com o ponerlos en comentarios y te los respondo.
Leer más