NÚMEROS COMPLEJOS

 









EJEMPLOS DE NÚMEROS COMPLEJOS





Dos números complejos son iguales si las partes reales son iguales y las partes imaginarias también son iguales .

Si a + bi = c + di  entonces  a = c  y  b = d.


Determina el valor de a y de b si:


(a + 6)+ 2bi= 6-5i

                            VALOR DE LAS POTENCIAS DE I




Operaciones con Números Complejos




RESOLVER


MULTIPLICACIÓN DE NÚMEROS COMPLEJOS




RESOLVER


Números complejos conjugados – Definición y ejemplos

Dos números complejos son conjugados si solo difieren en el signo de la parte imaginaria, entonces, a+bi y a-bi son números complejos conjugados.

Se acostumbra denotar al conjugado de un número complejo z como \bar{z}.

Los siguientes son ejemplos de números complejos conjugados:

Ejemplo 1:

z=1+i, \bar{z}=1-i

Ejemplo 2:

z=-2+5i, \bar{z}=-2-5i

Ejemplo 3:

z=-3-4i, \bar{z}=-3+4i

Ejemplo 4:

z=6+11i, \bar{z}=6-11i


RESOLVER


CUADRADO Y CUBO DE UN NÚMERO COMPLEJO

Sabemos que: 
- Cuadrado de un binomio (una suma/resta de dos términos, elevada al "cuadrado" o potencia segunda).

(a + b)2 = a2 + 2ab + b2

- Cubo de un binomio (una suma/resta de dos términos, elevada al "cubo" o potencia tercera)

(a + b)3 = a3 + 3a2b + 3ab2 + b3


Como los números complejos en su forma binómica tienen en general dos términos (uno real y el otro imaginario):

(a + bi)2

(a + bi)3

cuando se los eleva al cuadrado o al cubo se pueden aplicar esas fórmulas.


Ejemplo de cada uno:

Número complejo elevado al cuadrado:

(3 - 5i)2 =

32 + 2.3.(-5i) + (-5i)2 =

9 - 30i + (-5)2.i2 = 

9 - 30i + 25.(-1) =             (sabrás que i2 = -1)

9 - 30i - 25 = 

-16 - 30i


Número complejo elevado al cubo:

(-2 + 4i)3 =

(-2)3 + 3.(-2)2.4i + 3.(-2).(4i)2 + (4i)3 =

-8 + 3.4.4i + 3.(-2).16.i2 + 43.i3 =

-8 + 48i - 96.(-1) + 64.(-i) =              (sabrás que i3 = -i)

-8 + 48i + 96 - 64i =

88 - 16i

EJEMPLO










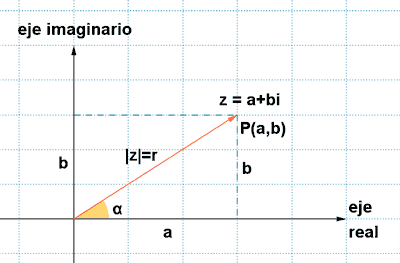
Argumento de un número complejo

Dado un número complejo   z = a + bi   llamamos argumento de   z   y lo expresamos como   arg z   al ángulo que forma el vector que lo representa con el semieje positivo del eje de abscisas (OX):


Expresión de un número complejo en forma polar

 x=r_{\alpha }

 \left | z \right |=r(r es el módulo)

 \textup{arg}(z)=\alpha (\alpha es el argumento)

 EJEMPLO:

z=1-\sqrt{3}i

 \left | z \right |=\sqrt{1^{2}+(-\sqrt{3})^{2}}=2

\alpha =\arctan \cfrac{-\sqrt{3}}{+1}=300^{\circ}

 Por lo tanto la forma polar de z=1-\sqrt{3}i es:

z=2_{300^{\circ}}

representacion grafica numero complejo

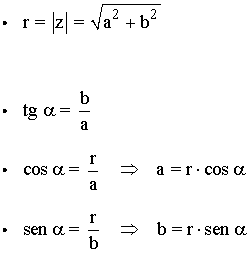
Paso de forma polar a forma binómica

Conocido un número complejo   z = rα   en forma polar, su forma binómica viene dada por:

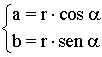
Es decir, el número complejo   z   puede expresarse de la siguiente manera:

Esta expresión recibe el nombre de forma trigonométrica.


Pasa a forma polar a la forma trigonométrica los siguientes números complejos:

Representa los siguientes conjuntos de números complejos. 
a) 5+2i
 b) -2 –i 
c) 3-4i 
d) -3+3i 
e) i 




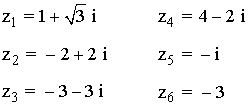
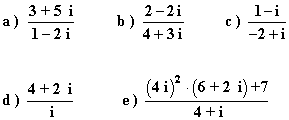
Comentarios

Publicar un comentario

Entradas más populares de este blog

Propiedades de la potenciación de números enteros

Imagen
Entonces, multiplicar potencias de igual base equivale a poner la misma base y sumar los exponentes. RESUELVE AHORA: ENTONCES, DIVIDIR POTENCIAS DE IGUAL BASE EQUIVALE A PONER LA MISMA BASE Y RESTAR LOS EXPONENTES.- Escribe en tu cuaderno los siguientes cocientes en forma de potencia:     a) 2 7  : 2 3           b) 3 5  : 3 3           c) 5 6  : 5 3 TIENES QUE SABER QUE SE PUEDE EXPRESAR LA DIVISIÓN DE POTENCIAS DE OTRA MANERA Y LA FORMA DE RESOLVER CUANDO TIENEN LA MISMA BASE, ES LA MISMA. AHORA OBSERVA  ASÍ, SI TENEMOS UNA POTENCIA ELEVADA A EXPONENTE, ES IGUAL A PONER LA MISMA BASE Y MULTIPLICAR LOS EXPONENTES. Escribe en tu cuaderno las siguientes potencias en forma de potencia con un solo exponente:     a) (2 3 ) 7           b) (3 5 ) 3           c) (5 5 ) 3 También podes acceder a: https://es.slideshare.net/logosacademyeduec/potenciacion-propiedades-eduardo Efectúa adecuadamente en tu cuaderno cada cas
Leer más

Ejercicios combinados con números decimales periódicos

Imagen
                                                                                                                             Realizar las siguientes operaciones realizando primero pasaje de decimal a fracción:   1)     2)     3)   Podés mandar tus resultados a luciasigrist@hotmail.com o ponerlos en comentarios y te los respondo.                                        
Leer más

Operaciones combinadas con potencias y raíces de fracciones

Imagen
Miramos detenidamente los vídeos, nos detenemos y hasta retrocedemos, en caso de no entender algo y después de haber comprendido o eliminado la duda, recién avanzar. No olvides escribir el o los ejercicios que se proponen en los vídeos en tu cuaderno, e ir resolviendo junto con el profesor.                                             Ahora resuelve:                                         Podés mandar tus resultados a luciasigrist@hotmail.com o ponerlos en comentarios y te los respondo.
Leer más