INTERÉS SIMPLE

OBSERVA CON MUCHA ATENCIÓN EL VÍDEO QUE SE DESARROLLA A CONTINUACIÓN, TOMANDO NOTAS DE LAS VARIABLES QUE SE PRESENTAN EN EL EJEMPLO Y REPITIÉNDOLO LAS VECES QUE SEAN NECESARIAS HASTA QUE COMPRENDAS EL CONCEPTO POR COMPLETO.

INTERÉS SIMPLE

En este caso los intereses que se generan en un periodo de tiempo no se agregan al capital para el cálculo de los intereses del siguiente periodo.

Su fórmula es la siguiente:

Interés simple = Capital * i * n

siendo “i” el interés nominal en tanto por uno (al expresarse habitualmente en tanto por ciento basta con dividir entre 100 para pasar a tanto por uno) y “n” el número de periodos.

La operación inversa al interés simple es el descuento simple que tiene mucha utilidad cuando invertimos en deuda pública o en pagarés, por comentar alguno de sus usos.

*Calcular el interés simple generado por 5000 € al 4% mensual durante 3 años.

En este caso, tenemos el tipo de interés expresado en meses y el periodo de tiempo en años. Por tanto, hay que pasar los años del periodo de tiempo a meses, para tener las dos cosas en la misma unidad.

Un año tiene 12 meses, por tanto, sólo hay que multiplicar 3 por 12, para obtener los 3 años en meses (también puedes hacerlo con un regla de tres):

Tiene sentido hacerlo así, porque el 4% mensual quiere decir, que el capital está generando intereses cada mes y por tanto hay que multiplicarlo por el número de meses que dura el préstamo par obtener el interés total.

OTRO EJEMPLO:

¿Durante cuántos años se ha colocado un capital de 2800 euros a un interés simple del 5% anual para tener al final de ese periodo un capital final de 3920 €?

En este caso nos dan como datos el capital inicial y el capital final, por lo que primero debemos calcular el capital generado, restando ambos capitales:

Ahora, aplicamos la fórmula del interés simple y sustituimos todos los valores que conocemos:

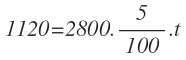
Y por último despejamos el tiempo:

La unidad del periodo de tiempo son años, ya que el tipo de interés es anual.

MAS EJEMPLOS:

*¿Cuál es el interés simple generado en un plazo fijo, por un capital de 10000 €, al 4% trimestral durante 2 años?

Aplicamos la fórmula del interés simple:

Pero tenemos en cuenta que el tipo de interés está en trimestres y el periodo de tiempo en años. Por tanto, debemos pasar los años a trimestres, multiplicando por 4, ya que un año tiene 4 trimestres:

*Hace 4 años de pidió un préstamo de 7000 € y la cantidad pagada al terminar el periodo del préstamo han sido 9500 €. ¿Qué tipo de interés se le aplicó?

En este caso el capital inicial son 7000 €, pero cuidado, porque los intereses generados no son 9500 €. Los 9500 € corresponden al capital final.

Por tanto, calculamos los intereses generados en primer lugar:

Ahora sustituimos todos los datos en la fórmula del interés simple:

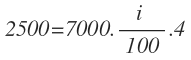
Y despejamos el tipo de interés:

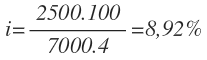
Es un tipo de interés anual, ya que el periodo de tiempo estaba en años.

*

*Después de 3 años, un banco ha pagado en concepto de interés la cantidad de 840 € a una persona por depositar un plazo fijo. La tasa de interés ha sido del 2% anual. ¿Cuál fue el capital inicial con el que se hizo el depósito?

En este caso, conocemos todo menos el capital inicial.

Sustituimos en la fórmula:

Y despejamos el capital inicial:

*¿Durante cuánto tiempo ha de imponerse un capital de 25 000 € al 5% para que se convierta en 30.000 €?

 Notemos que tenemos el capital final y el capital inicial. Por lo tanto, primero debemos calcular el interés que debemos obtener:

 

 Una vez que tenemos el interés que deseamos obtener, entonces calculamos el tiempo utilizando:

 

 Por lo tanto, el tiempo requerido es 4 años.

*Se prestan 45 000 € y al cabo de un año, 4 meses y 15 días se reciben 52 500 €.

Calcular el interés como porcentaje.

 Calculamos el tiempo en días

 

 Calculamos el interés

 

Calculamos la tasa de interés:

 

 No obstante, esta es la tasa diaria de interés. Para tener la tasa anual debemos multiplicar por 365. Además, para tener la tasa como porcentaje, debemos multiplicar por 100:

 

 Así, la tasa de interés es del 12.16% anual.

*Hallar la tasa de interés simple (como porcentaje) al que deberá prestarse un capital para que al cabo de 20 años los intereses sean equivalentes al capital prestado.

 Solución:

Deseamos que el interés sea igual al capital, es decir,

 

 En la fórmula para calcular  sustituimos el interés por :

 

 Como el capital es distinto de 0, entonces cancelamos  de ambos lados de la ecuación:  

 Despejamos la tasa de interés:

 

 Sabemos que el tiempo es de 20 años, por lo tanto, tenemos:

 

 De este modo, la tasa de interés es 0.05. Escrito de forma porcentual, la tasa de interés es del 5%.

*¿En cuánto tiempo el interés será igual al triple del capital inicial colocado a una tasa de interés al 6%?

 Solución:

Necesitamos, ahora, que el interés sea igual al triple del capital inicial, es decir,

 

 Sustituimos este interés en la fórmula que se utiliza para calcular :

 

 Cancelamos  y despejamos :

 

 Sustituimos la tasa de interés, recordando que una tasa del 6% es igual a :

 Por lo tanto, el tiempo es de 50 años.